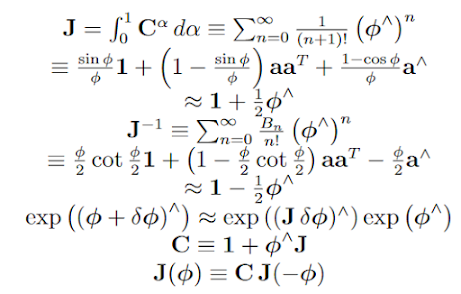本文為 State Estimation for Robotics 書中第 7.1 節 Matrix Lie Groups Geometry 的筆記。讀者可以先參考前文:
定義 left Jacobian
先定義 se(3) \(\xi\) 與其對應的 SE(3) \(\mathbf{T}\),兩者的關係式為: \[ \mathbf{T}={exp}(\xi)^{\wedge} \\ \xi = {ln}(\mathbf{T})^{\vee} \\ {exp}(\xi)^{\wedge} = \sum_{n=0}^{\infty}\frac{1}{n!}(\xi^{\wedge})^n = \sum_{n=0}^{\infty}\frac{1}{n!}( \begin{bmatrix} \rho \\ \phi \end{bmatrix}^{\wedge} )^n =\sum_{n=0}^{\infty}\frac{1}{n!}( \begin{bmatrix} \phi^{\wedge} & \rho\\ \mathbf{0}^T & 0 \end{bmatrix} ^{\wedge} )^n \\ =\begin{bmatrix} \sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n & (\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^n)\rho\\ \mathbf{0}^T & 1 \end{bmatrix} =\begin{bmatrix} \mathbf{C} & \mathbf{r}\\ \mathbf{0}^T & 1 \end{bmatrix} = \mathbf{T} \in SE(3) \]其中 \(\mathbf{r}\) 即為三維空間中的平移,其與 se(3) \(\xi\) 中的參數 \(\rho\) 的關係為 \(\mathbf{r} = \mathbf{J}_l\rho\),在此定義了 SO(3) 的 left Jacobian \(\mathbf{J}_l\)。
Left Jacobian 的性質
以下截圖取自於參考資料 [1]:
定義 Adjoints
SE(3) 的 adjoint 為一個 \(6 \times 6\) 的矩陣: \[ \mathfrak{T}=Ad(\mathbf{T})=\begin{bmatrix} \mathbf{C} & \mathbf{r^{\wedge}C}\\ \mathbf{0} & \mathbf{C} \end{bmatrix} \]其很多性質皆與 se(3)、SE(3) 的性質類似。
Baker-Campbell-Hausdorff 公式
實數的指數函數相乘為 \(exp(a)exp(b)=exp(a+b)\),但矩陣的指數變換下此式子並不成立。BCH 公式寫出了 \(ln(exp(\mathbf{A})exp(\mathbf{B}))\) 的解,而由於 BCH 公式是個無窮級數,因此我們通常使用的是 BCH 公式的近似式。
在 SO(3) 的情況下此近似式可以寫成: \[ ln(\mathbf{C_1C_2})^{\vee}=ln(exp(\phi_1^{\wedge})exp(\phi_2^{\wedge}))^{\vee} \\ \approx \left\{\begin{matrix} \mathbf{J}_l(\phi_2)^{-1}\phi_1+\phi_2\\ \mathbf{J}_r(\phi_1)^{-1}\phi_2+\phi_1 \end{matrix}\right. \]參考資料 [1] 中有更多 left Jacobian 與 right Jacobian 的定義。在 SE(3) 也有類似的性質,書中與參考資料中都有更詳細的推導過程。
李群之間的距離
兩個旋轉矩陣的距離可以用以下式子定義: \[ \phi_{12}=ln(\mathbf{C}^T_1\mathbf{C}_2)^{\vee} \\ \phi_{21}=ln(\mathbf{C}^T_2\mathbf{C}_1)^{\vee} \]而 so(3) 的內積可以定義成:\(\left \langle \phi_1^{\wedge},\phi_2^{\wedge} \right \rangle=-\frac{1}{2}tr(\phi_1^{\wedge}\phi_2^{\wedge T})=\phi_1^T\phi_2\)。當有很小的擾動 \(\delta \phi\) 時,新的旋轉矩陣為 \(\mathbf{C}'=exp((\phi+\delta \phi)^{\wedge})\),與原本的旋轉矩陣的距離可以分別寫成左邊與右邊的距離: \[ ln(\delta \mathbf{C}_r)^{\vee}\approx \mathbf{J}_r\delta \phi \\ ln(\delta \mathbf{C}_l)^{\vee}\approx \mathbf{J}_l\delta \phi \]儘管分成左與右距離,但兩者的 volume 完全相同。
李群的內插
SO(3) 或 SE(3) 無法直接線性內插,因此得用此式子來內插兩個旋轉矩陣:\[\mathbf{C}=(\mathbf{C}_2\mathbf{C}_1^T)^\alpha\mathbf{C}_1 \\ \alpha \in [0, 1]\]用 BCH 公式近似後為以下式子:\(\alpha \mathbf{J}(\phi_1)^{-1}\phi_{21}+\phi_1\)。另外書中也提到微小的旋轉變化式子 (7.137)。
李群的微分
可以參考前文:三維空間轉換與李理論(六)。