本文將介紹兩篇 deep fundamental matrix estimation 的 paper。Fundamental matrix 的介紹可以參考前文:
- Epipolar Geometry:介紹 essential matrix 及 fundamental matrix
- 關於 Essential Matrix 與 Homography Matrix 的更多筆記
Deep Fundamental Matrix Estimation
本文提出來的方法是用來解決 model fitting 的問題,而用 fundamental matrix estimation 當成一個用例。
一般來說一個 model fitting 問題可以寫成以下形式:
而為了處理 outlier 的情形,會在式子中針對每個 sample 加入不同的 weight,再利用迭代找出最佳解:
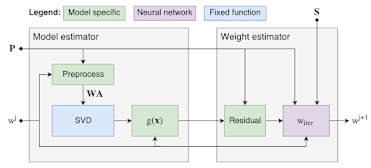
本文的方法為上圖迭代解的延伸,也就是利用類神經網路學出 weight 的分布,再利用迭代法算出解:
上圖可寫成以下演算法:接著只要定義模型中的式子即可。拿 fundamental matrix 來說:
- Residual 為 Symmetric epipolar distance
- Loss function 為利用估計出來的 F 算出來的 symmetric epipolar distance
- Model extractor g(x) 必須滿足 fundamental matrix 的幾何特性
Deep Fundamental Matrix Estimation without Correspondences
這篇文章的方法很直覺,主要包含兩個步驟:
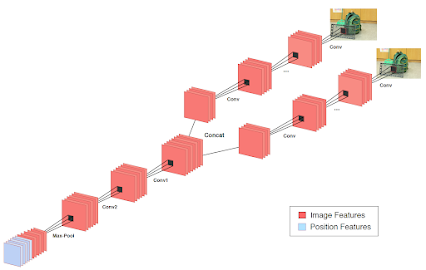
- Siamese Architecture 將兩張圖分別的 feature map 結合在一起成為新的 feature map
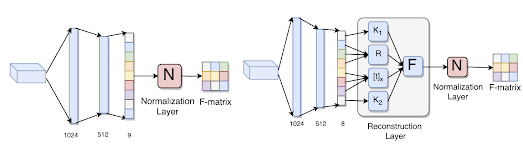
- 利用 fully connected layer 算出 fundamental matrix 的每一項,包含了兩種方法
- 直接計算,但算出來的 fundamental matrix 不一定能滿足其幾何性質。
- 利用 F-matrix Reconstruction Layer 加入 fundamental matrix 的幾何特性。
參考資料
[1] Deep Fundamental Matrix Estimation
[2] Deep Fundamental Matrix Estimation without Correspondences
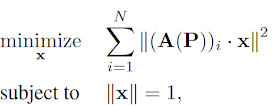


沒有留言:
張貼留言