Lucas-Kanade 演算法的各種變形

本文要介紹的是用於計算 optical flow 的 Lucas-Kanade 演算法的四種變形，主要參考於資料 [1]。前文中大致介紹了概念，本文將深入更多細節。

以下為 Lukas-Kanade 演算法的示意圖：

這是最常見的作法，其想要最佳化的目標為： \[ \sum_{\mathbf{x}}[I(\mathbf{W}(\mathbf{x};\mathbf{p})) - T(\mathbf{x})]^2 \]這個式子的意義是將 template 圖片在用參數 p 轉換後的圖片 I 上面找到對應的位置。Warping 的參數 p 的例子為平移、affine transform 等等。此式子的解是利用一階泰勒展開式： \[ \sum_{\mathbf{x}}[I(\mathbf{W}(\mathbf{x};\mathbf{p}+\mathbf{\Delta p})) - T(\mathbf{x})]^2 \]再藉由算出 \(\Delta p\) 後更新 p 的值：\(p = p + \Delta p\)，因此本方法也稱為 forward additive 方法。要注意的是此方法花最多時間的部分是計算 Hessian 矩陣。

第二種方法為 forward compositional 的方法，其想要最佳化的目標為： \[ \sum_{\mathbf{x}}[I(\mathbf{W}(\mathbf{W}(\mathbf{x};\mathbf{\Delta p});\mathbf{p})) - T(\mathbf{x})]^2 \]意思是說如果加入 \(\Delta p\) 以後的變換 W(x; \Delta p) 可以使得此函數的值變小，則我們要將此變換更新：\(W(x;p)=W(x;p) \cdot W(x; \Delta p)\)這個方法的好處是 Jacobian 矩陣只要算一次即可，但是仍得花大部分時間計算 Hessian 矩陣。

第三種方法為 inverse compositional 的方法，其最佳化的目標為： \[ \sum_{\mathbf{x}}[T(\mathbf{W}(\mathbf{x};\mathbf{\Delta p}))-I(\mathbf{W}(\mathbf{x};\mathbf{p}))] \]假如一開始 T(x) 與 I(W(x; p)) 對應，在 T 上的點經由 \(W(x; \Delta p)\) 轉換以後會對應到最佳的 I(W(x; p))，因此最佳解為反向操作：\( W(x;p) = W(x;p) \cdot W(x; \Delta p)^{-1}\)，這樣就能最佳化此函數。這個方法的理解比較困難，因此附上資料 [2] 供參考。

第四種方法為 inverse additive 的方法，最佳化的目標與 forward additive 相同，但是找出最佳解的方法不同。此方法有機會降低 Hessian 矩陣的計算複雜度。

四種方法的比較

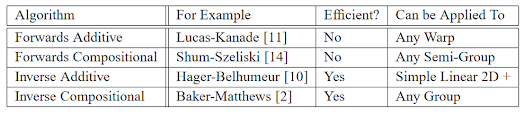
下圖為四種方法的比較：

可以看出 forward additive 雖然比較慢，但是較少限制。Inverse additive 雖然可以跑得很快，但只能用在簡單的 warp 之上。另外雖然四種方法理論上都是等價的，但實務上兩種 forward 的演算法比較穩定。

參考資料

[1] Lucas-Kanade 20 Years On: A Unifying Framework: Part 1

[2] SVO中 Inverse Compositional Image Alignment方法的学习笔记