先複習以前寫過的相關文章:
- 三維空間旋轉
- 關於三維空間轉換的更多筆記
- Quaternion 四元數簡介
- 李群、李代數與三維空間旋轉 Lie Group & Lie Algebra
- SO(3) 上的李代數求導數
- 三維空間轉換與李理論(一)
- 三維空間轉換與李理論(二)
- 三維空間轉換與李理論(三)
本文將以參考資料 [1, 2] 的內容為基礎整理出一份完整的筆記。
用兩個例子介紹李群
一個群滿足了 closure、associativity、identity、inverse 四個條件(註:不保證 commutative )。而李群為具有連續性質的群。
S1:單位複數
假設 \(z\) 為一個單位複數,其滿足以下性質:
- Topology 為單位圓。
- 空間的兩個軸為 1 與 i。
- \(y = z \cdot x\) 的意義為旋轉複數 \(x\),而運算子 \(z\) 即為李群的一項。
- \(z\) 的數學式為 \(z = cos \theta + i\ sin \theta\)。
- \(z\) 的 inverse 為 \(z^*\)。
- Composition 為 \(z_1 \cdot z_2\)。
SO(2):2D 旋轉矩陣
假設 \(R\) 為一個 2D 旋轉,其滿足以下性質:
- Topology 為一個圓。
- 空間的兩個軸為 \(I_{2 \times 2}\) 與 \([1]_x\)。\[ [1]_x=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \]
- \(y = R \cdot x\) 的意義為將二維向量 x 旋轉至另一個二維向量 y,而此運算子 \(R\) 為此李群的一項。
- \(R\) 的數學式為 \(R = I_{2 \times 2}\ cos \theta + [1]_x\ sin \theta\)。
- \(R\) 的 inverse 為 \(R^T\)。
- Composition 為 \(R_1 \cdot R_2\)。
其他更多的例子可以參考 [3]。
李理論的拓樸學
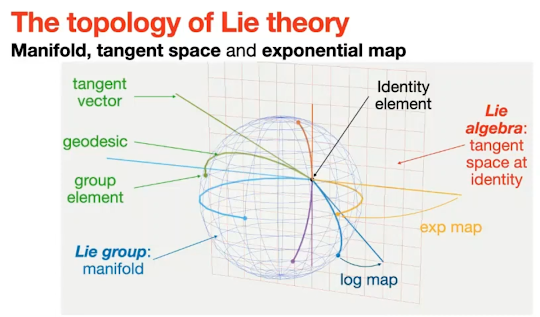
上圖為 [2] 的作者 Joan Solà 的影片 [4] 中的圖。這張圖描述了李群與李代數的關係:
- 李群為光滑的流形。
- 李代數為李群在 identity 的切線空間,也就是描述了李群在 identity 附近的局部性質。
- exp map 為李代數 \(\mathbb{M}\) 至李群 \(\mathbb{T}\) 的轉換。
- log map 為李群 \(\mathbb{T}\) 至李代數 \(\mathbb{M}\) 的轉換。
- 切線空間 tangent space 為向量空間,因此可以在其上做微積分,而在李群上不行,這也就是為什麼李理論被廣泛用在三維空間轉換之中。
- 切線空間的維度為對應的流形 manifold 的自由度。
- hat operator (\(\wedge\)) 是將切線空間上的向量空間轉換成李代數。
- vee operator (\(\vee\)) 是將切線空間上的李代數轉換成向量空間。
切線空間的例子:S1
剛剛說過李代數為李群在 identity 的切線空間,而 S1 的 identity 為 1,因此我們要找出在 1 的切線空間。當然從幾何直覺上我們知道切線空間為 \(i\omega\),\(\omega\) 為任意實數,\(i\omega\) 會與 1 的軸垂直。而從代數上我們可以解以下微分方程: \[ z^* \cdot z = 1 \\ \dot{z}^*z+z^*\dot{z}=0 \\ z^*\dot{z}=-(z^*\dot{z})^* \]因此 \( z^*\dot{z}\) 一定是 \(i\omega\),而由於 \(z^*=z=1\),所以切線空間 \(\dot{z}\) 即為 \(i\omega\) 了。而其對應的向量空間表示為 \(\omega\),因此在此例子中我們可以定義其 hat 與 vee operators:
- hat: \(\omega^{\wedge}=i \cdot \omega\)
- vee: \(\omega=(\omega^{\wedge})^{\vee}=-i\cdot \omega^{\wedge}\)
參考資料
[2] A micro Lie theory for state estimation in robotic
[4] Lie theory for the roboticist
沒有留言:
張貼留言