Hermite Splines 及 2D 曲線模型簡介

本文要介紹的是如何用數學模型在電腦中產生曲線。首先來討論曲線模型的需求：

• Local control：曲線模型是由數個控制點來生成的。我們希望當移動控制點時只會改變整個曲線軌跡的一小部分，而不是整條曲線軌跡；這樣會讓我們修改曲線時更簡單。
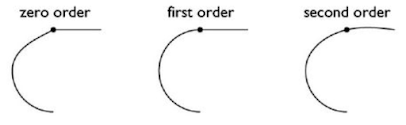
• Smoothness & continuity：有三種連續性的定義，下圖出自於 [1]。
  
• C0：點的座標連續
  
• C1：點的斜率連續
• C2：點的曲率連續

• Affine invariance：控制點經由 affline 變換以後產生的曲線與直接將曲線 affine 變換後的曲線重合。

Hermite Splines

Hermite Splines 直接針對 C0 及 C1 的連續性限制來產生局部曲線，也就是針對每一小段曲線的端點其座標與斜率都得連續，推導式子如下： \[ x(t) = at^3+bt^2+ct+d \\ x'(t) = 3at^2 + 2bt + c \\ x(0) = d\\ x'(0) = c\\ x(1) = a+b+c+d\\ x'(1) = 3a+2b+c\\ \] 因此在整理過後，在給定兩端的座標 \(x_0, x_1\) 及斜率 \(x'_0, x'_1\) 後我們就可以用以下式子求出此局部曲線的係數 \(a,b,c,d\)： \[ a=2x_0-2x_1+x'_0+x'_1\\ b=-3x_0-3x_1-2x'_0-x'_1\\ c=x'_0\\ d=x_0\\ \] 或是把整段寫成矩陣式子： \[ x(t) = \begin{bmatrix} t^3 &t^2 &t &1 \end{bmatrix} \begin{bmatrix} 2 &-2 &1 &1 \\ -3 &3 &-2 &-1 \\ 0 &0 &1 &0 \\ 1 &0 &0 &0 \end{bmatrix} \begin{bmatrix} x_0\\ x_1\\ x'_0\\ x'_1 \end{bmatrix} \] 將左邊兩個矩陣相乘起來後可得： \[ x(t) = \begin{bmatrix} 2t^3+3t^2+1\\ -2t^3+3t^2\\ t^3-2t^2+t\\ t^3-t^2 \end{bmatrix}^T \begin{bmatrix} x_0\\ x_1\\ x'_0\\ x'_1 \end{bmatrix} \] 這四個多項式即為 Hermite Spline 的 basis function。下圖取自於 [3]，為 Hermite Spline 的 basis function 示意圖： 

Hermite Splines 的一些性質

• 利用端點的位置及斜率來決定局部曲線，這些端點即為 Hermite Spline 的控制點，又稱 knots。
• Hermite Splines 為 C1 連續性。
• Hermite Splines 的主要問題是需要給定端點的斜率，在實作上不是很方便，因此在之後的文章會介紹其他種曲線模型來解決此問題。
  

參考資料

[1] 2D Spline Curves

[2] Curves and Splines

[3] 2D Spline Curves CONT'D