Catmull-Rom Splines、Bezier Splines 的 2D 曲線模型簡介

我們在前文簡介了 Hermite Splines。Hermite Splines 的問題是我們必須給定兩個端點的斜率 \(x'_0, x'_1\)，在實作上並不是這麼直觀，因此 Catmull-Rom Splines 的設計就是要讓計算斜率的過程更直觀。

用一句話就可以解釋 Catmull-Rom Splines 怎麼計算斜率─前後兩個控制點的內插結果即為此控制點的斜率，也就是說：\[p'_i = s(p_{i+1}-p_{i-1})\]而當我們假設這個系統裡有四個控制點\(q_{k-1}, q_k, q_{k+1}, q_{k+2}\) 時，並假設 \(q_k\) 與 \(q_{k+1}\) 為前文 Hermite Splines 中的兩個端點，我們即可用以下式子來推導出 \(q_k\) 與 \(q_{k+1}\) 的斜率： \[ x_0 = q_k \\ x_1 = q_{k+1} \\ x'_0 = s(q_{k+1}-q_{k-1}) \\ x'_1 = s(q_{k+2}-q_{k}) \\ \] 因此將上面式子與 Hermite Splines 的式子結合在一起就能得到 Catmull-Rom Splines 的參數式： \[ x(t)=\begin{bmatrix} t^3 &t^2 &t &1 \end{bmatrix} \begin{bmatrix} 2 &-2 &1 &1 \\ -3 &3 &-2 &-1 \\ 0 &0 &1 &0 \\ 1 &0 &0 &0 \end{bmatrix} \begin{bmatrix} 0 &1 &0 &0 \\ 0 &0 &1 &0 \\ -s &0 &s &0 \\ 0 &-s &0 &s \end{bmatrix} \begin{bmatrix} q_{k-1}\\ q_k\\ q_{k+1}\\ q_{k+2} \end{bmatrix}\\ = \begin{bmatrix} t^3 &t^2 &t &1 \end{bmatrix} \begin{bmatrix} -s &2-s &s-2 &s \\ 2s &s-3 &3-2s &-s \\ -s &0 &s &0 \\ 0 &1 &0 &0 \end{bmatrix} \begin{bmatrix} q_{k-1}\\ q_k\\ q_{k+1}\\ q_{k+2} \end{bmatrix} \]以下為參考資料 [1] 的示意圖：

Bezier Splines

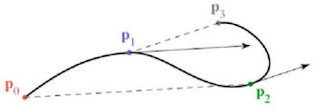
Bezier Splines 是另一種與 Hermite Splines、Carmull-Rom Splines 等價的曲線模型。在此模型中每段曲線有四個控制點（註：我們假設的是三次 Bezier Splines。），\(p_0\) 與 \(p_3\) 在曲線上，而 \(p_1\) 與 \(p_2\) 不在曲線上。Bezier Splines 直接用 \(p_1\) 與 \(p_2\) 的位置來決定兩個端點 \(p_0\) 與 \(p_3\) 的斜率： \[ x_0 = p_0 \\ x_1 = p_3 \\ x'_0 = 3(p_1 - p_0) \\ x'_1 = 3(p_3 - p_2) \] 這個係數 3 是怎麼決定的我仍不太明白，但我目前的解釋是為了寫出 Bezier Splines 的一般式，也就是用 Bernstein polynomial 的係數來寫出 N 次的 Bezier Splines。

解出來的曲線參數式如下： \[ x(t) = \begin{bmatrix} t^3 & t^2 & t & 1 \end{bmatrix} \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 &-6 &3 &0 \\ -3 &3 &0 &0 \\ 1 &0 &0 &0 \end{bmatrix} \begin{bmatrix} p_0\\ p_1\\ p_2\\ p_3 \end{bmatrix} \] 

Bezier Splines 的一些性質 

• Bezier Splines 為 C1 連續性
• 可以用 De Casteljau's algorithm 來建構 Bezier Splines。細節請參考 wikipedia [3]。
  

參考資料

[1] 2D Spline Curves CONT'D

[2] Curves and Splines 

[3] Bezier curve