我們在前文簡介了 Hermite Splines、Catmull-Rom Splines 以及 Bezier Splines。本文要介紹的是另一種曲線模型 B-Splines。
三次方的 Hermite、Catmull-Rom、Bezier Splines 都只能達到 C1 連續性,都無法滿足 C2 連續性(也就是 curvature 的連續)的要求,而如果想要滿足的話有幾種可能性:
- 用更高次方的曲線模型,但是計算會變得更複雜。
- 放棄 local control 的要求:natural cubic splines 便是一種無法滿足 local control 要求的曲線模型。
- 放棄用端點來生成內插曲線的要求:B-Splines 便是放棄此要求。前文所介紹的曲線模型,以及 natural cubic splines 的曲線都會經過端點,但是 B-Splines 只能保證曲線會很接近端點。
因此對於三次方的曲線模型來說,C2 連續性、local control 以及內插曲線三種要求只能滿足其二。
建構 B-Splines 曲線
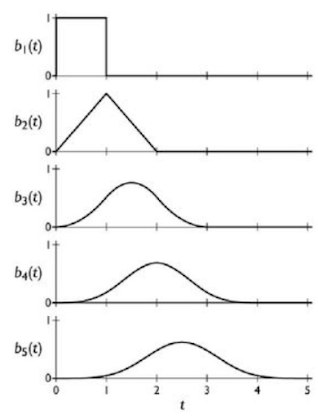
假如有 N 段曲線的話,需要 N+3 個控制點。我們可以用 Cox-deBoor 演算法來產生B-Splines 曲線: \[ b_1 = \left\{\begin{matrix} 1\quad 0\leq u < 1 \\ 0\quad otherwise \end{matrix}\right. \\ b_d =\frac{t}{d-1} b_{d-1}(t)+\frac{d-t}{d-1}b_{d-1}(t-1) \] 下圖為參考資料 [1] 的示意圖:
可以看出每一層 \(b_d\) 都是將前一層 \(b_{d-1}\) 變得更平滑後的結果。
最後要提到的是 B-Splines 的矩陣表示式: \[ p(t)= \begin{bmatrix} t^3 &t^2 &t &1 \end{bmatrix} \cdot \frac{1}{6} \begin{bmatrix} -1 &3 &-3 &1 \\ 3 &-6 &3 &0 \\ -3 &0 &3 &0 \\ 1 &4 &1 &0 \end{bmatrix} \begin{bmatrix} p_{k-1}\\ p_{k}\\ p_{k+1}\\ p_{k+2} \end{bmatrix} \]
參考資料
[1] B-Splines
沒有留言:
張貼留言