PointNetLK 簡介：找出點雲之間的幾何變換關係

本篇文章要介紹的是 PointNetLK [1]，目的是利用深度學習的方法找到兩個點雲之間的平移旋轉關係，在英文文獻中的術語是 Point set registration [2]。我們一般可以用 Iterative closest point (ICP) [3] 演算法來解決這個問題，但是 ICP 演算法有一些限制：

• 當點的數目多的時候要跑很久
• 對初始值很敏感

 

PointNetLK 的精神

先假設以下的變數：

• \(P_S\)：輸入的點雲。
• \(P_T\)：想要找出平移旋轉關係的參考點雲。
• \(G\)：平移旋轉的矩陣，一般我們用 \(3 \times 3\) 的矩陣描述三維空間旋轉，以及三維向量描述平移，但為了計算方便我們通常用 \(4 \times 4\) 的矩陣來表示 \(G\)。
  
• \(\phi\) 函數：輸入為點雲，輸出為一個代表點雲特徵向量的函數。

這個問題的目標是找到一組平移旋轉關係 \(G\) 使得變換後的 \(P_S\) 與 \(P_T\) 之間的差異越小越好，而當這兩個點雲的差異小的話那他們對應的特徵向量差異也會小，也就是以下關係： \[ \phi(P_T) = \phi(G \cdot P_S) \] 

PointNetLK 的一些式子推導

1. \(\phi(P_S) = \phi(G^{-1} \cdot P_T)\)，上式與此式等價。
2. 利用泰勒展開式近似等號右邊： \[ \phi(P_S) = \phi(P_T) + \frac{\partial }{\partial \xi}[\phi(G^{-1} \cdot P_T)]\xi \] 
3. 前面提到 G 是描述平移旋轉的矩陣，也就是 SE3。我們用李代數與李群的指數映射關係來表示 G，\(\xi\) 為 G 對應的李代數，可以用個六維向量來表示： \[ G^{-1}=exp(-\sum_i \xi_i T_i) \] 
4. 我們用 \(J\) 表示上面的 \(\frac{\partial }{\partial \xi}[\phi(G^{-1} \cdot P_T)]\)，也就是 Jacobian。
5. 因此當解出 \(\xi\) 時就能算出對應的 SE3（\(G\)），也就是旋轉平移的關係。而 \(\xi\) 可用以下式子來求出： \[ \xi = J^+ [\phi(P_S) - \phi(P_T)] \] 
6. \(J^+\) 為 J 的 Moore-Penrose inverse。
7. 拿新的 \(\xi\) 算出對應的 G，更新 \(P_S\)，再算下一輪，直到這一輪的 G 更新小於一個數字。
8. 在訓練時的 loss function 為： \[ L = \left \| (G_{est}^{-1} \cdot G_{gt})-I_4 \right \|_F \]
   

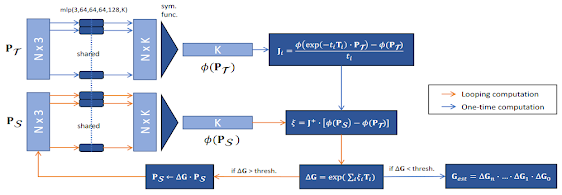
 以下為 PointNetLK 的架構圖：

PointNetLK 的實作細節

1. 函數 \(\phi\) 是 Pointnet 的 feature，維度是 \(B \times K\)，B 是 batch size，K 為特徵向量的維度。
   
2. Jacobian J 的維度是 \(B \times K \times 6\)，6 代表李代數 \(\xi\) 的六個維度，而圖中的 \(t_i\) 代表李代數 \(\xi_i\) 的微小變化。
3. \(J^+\) 的維度是 \(B \times 6 \times K\)。
4. 圖中的 exp 為前文介紹的指數映射。
   

參考資料

[1] PointNetLK: Robust & Efficient Point Cloud Registration using PointNet

[2] Point set registration 

[3] Iterative closest point