這篇文章要談的是抽樣方法(Sampling)。在實務上往往我們的機率模型非常複雜,而抽樣方法想做的事情是從這個複雜的機率模型中產生樣本,當然產生的樣本必須符合這個機率分布。打個比方,在產生隨機號碼的時候我們就是想要從 uniform distribution 中產生一個樣本,然後再根據需求來放大或平移,而所有生成出來的隨機號碼必須符合 uniform distribution。在抽樣時我們考慮的是此機率模型的機率密度函數 probabilistic density function 有沒有辦法積分成累積分布函數 cumulative distribution function,如果沒辦法直接積分的話則可以用其他方法,像是 Rejection Sampling 來產生樣本。
從可積分的機率密度函數中產生樣本
要產生樣本之前,我們先假設有一個符合 uniform distribution 的隨機數字產生器,能隨機產生 0 到 1 之間的任何數字。而對於任意的機率密度函數來說,我們只要先求得其累積分布函數,將此隨機數字代進去,再轉換為機率密度函數,那麼就產生了一個符合這個機率模型的樣本了。假設此機率模型的機率密度函數為 p(x),並且我們令其累積分布函數為 h(y),則兩者的關係為: \[ h(y)\equiv \int_{- \infty}^{y}p(x)dx \]在以上式子中 x 的範圍是負無限大至正無限大,而 y 的範圍是 0 到 1。因此當想要產生樣本時,我們先用 uniform distribution 產生一個 0 到 1 中間的數字 y,再代進去累積分布函數的反函數 \(h^{-1}(y)\),得到的結果即為符合機率密度函數 p(x) 的樣本了。
例子:指數分布
對於指數分布不熟悉的讀者可以先看以前的文章。指數分布的機率密度函數為:
\[
p(x)=\lambda\ exp(-\lambda x)
\]
而指數分布的累積分布函數 h(y) 為:
\[
h(y)\equiv \int_{- \infty}^{y}p(x)dx = \int_{0}^{y}\lambda\ exp(-\lambda x) dx
\\
= \lambda\ \frac{-1}{\lambda}exp(-\lambda x)\mid^y_0
\\
= 1 - exp(-\lambda y)
\]
由上式可以推得 h(y) 的反函數:
\[
x = h(y)^{-1} = -\frac{ln(1-y)}{\lambda}
\]
意思就是先用 uniform distribution 生成 0 到 1 之間的 y,代入到上式,即可產生一個符合指數分布的樣本 x 了。
Rejection Sampling:從無法計算積分的複雜機率函數中產生樣本
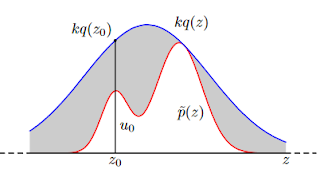
用一張示意圖會比較容易解釋 Rejection Sampling。這張示意圖是 Pattern Recognition And Machine Learning 書中的 Figure 11.4:
上圖中我們想要從機率密度函數 \(\tilde{p}(z)\) 產生樣本。我們選一個非常熟悉的機率分布 q(z)(像是圖中的高斯分布),並且乘以一個常數 k,使得 \(\tilde{p}(z)\) 完全被 \(kq(z)\) 涵蓋。接下來我們從 q(z) 中產生一個樣本 \(z_0\),而 \(p(z_0)=u_0\)。再從 uniform distribution 中產生一個隨機數字 U,如果 U 滿足以下條件則 \(z_0\) 即為產生的樣本,否則就重來一次:
\[
U < \frac{u_0}{kq(z_0)}
\]這個演算法的正確性證明可以參考華盛頓大學 Yen-Chi Chen 老師的講義[1]。
Importance Sampling:從無法計算積分的複雜機率函數中計算期望值
有時候我們想要取得樣本的原因是可以計算此機率分布的期望值。Importance Sampling 是近似複雜機率模型期望值的一個方法,但是它無法拿來產生單獨的樣本,而這就是 Importance Sampling 與 Rejection Sampling 最主要的差別。
回到期望值計算,在求期望值時我們想要的計算以下式子:
\[
E[f]=\int f(x)p(x)dx
\]
上式中 x 是隨機變數,而 p(x) 是機率密度函數。Imporance Sampling 的方法是先挑一個容易產生樣本的機率密度函數 q(x),然後代入期望值的式子:
\[
E[f] = \int f(x)p(x)dx = \int f(x) \frac{p(x)}{q(x)}q(x)dx
\\
\simeq \frac{1}{L}\sum_{i=1}^{L}\frac{p(z_i)}{q(z_i)}f(z_i)
\]
上式的意思是從 q(x) 代表的機率分布中產生 L 個 IID 樣本 \(z_i\),就能用以上式子估計出期望值 E[f]。在上式中 \(r_i=p(z_i)/q(z_i)\) 稱為 importance weight,意思是當 \(r_i\) 很大時代表在此時 \(p(z_i)\) 大於 \(q(z_i)\),因此我們就給它比較大的權重,就好像是 \(z_i\) 這個樣本在原本的機率模型中出現比較多次。而當 \(r_i\) 很小的時候就做相反的事情,給它很小的權重就好像是它在原本的機率模型中很少出現。
此外值得一提的是 Importance Sampling 估計出來的期望值是無偏估計 Unbiased estimator。(註:需要複習無偏與有偏估計的讀者可以看我以前的文章。)其他細節也請參考 Yen-Chi Chen 老師的講義。
參考資料
[1] Importance Sampling and Rejection Sampling, Yen-Chi Chen
沒有留言:
張貼留言